递归递推

时间复杂度：看for的n，取最大

空间复杂度：看实际运行的时候用到了多少内存。

在递归算法中，每次递推都需要一个栈空间来保存调用记彔，因此在计算空间复杂度时需要计算递归栈的辅助空间。

对于递推和递归来说，其实是完全不同的两个思路

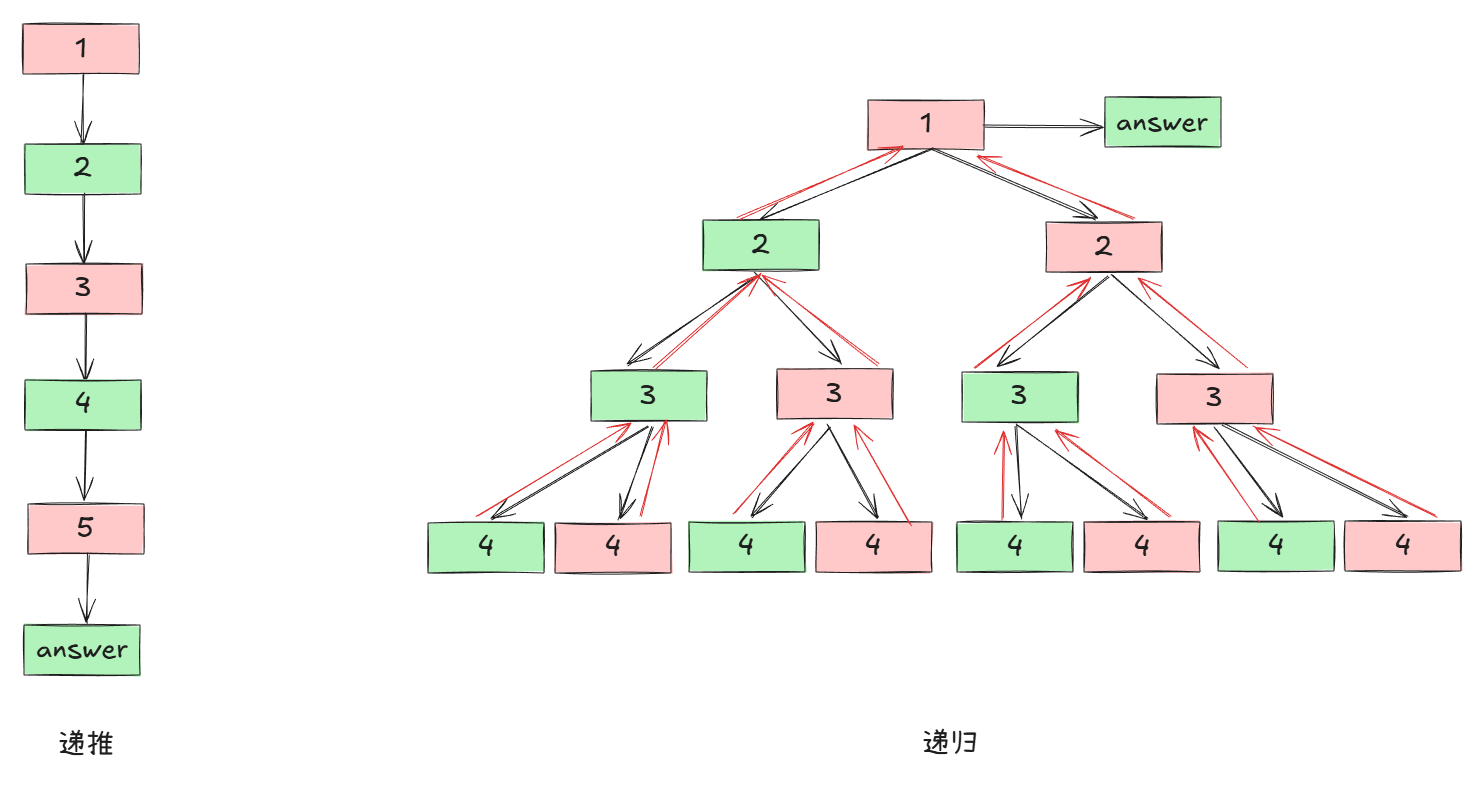
递归是“一个实体调用自身” 。这具体表现为一个函数直接或间接调用自身，以解决一个给定问题的更小实例。递归的本质在于“自我参照”。
递推在此上下文中被理解为迭代计算过程。迭代的定义是“重复执行一组指令” ，通常通过循环结构（如 for, while 或 do-while）来实现。递推的本质在于“重复” 。

我们可以从多个角度去看待递归和递推，比如说从传入参数的显式和隐式：

递归：隐式的使用调用栈来存储中间变量（如局部变量、参数、执行进度），我们只需要写问题如何分解的
递推：显式的通过循环计数器、累加器、指针，或在复杂情况下使用显式数据结构（如栈或队列）来手动管理计算状态，我们需要规定状态如何演变

从自上到下和自下到上的设计逻辑来说：

递归：在DP中是自顶向下对状态空间进行搜索和记忆化
递推：在循环中从最小的解开始，“自底向上”地逐步计算和组合，直到构建出更大规模问题的解。

从并行的角度来看：

递归：从分治的角度来看，天然把任务分成更多的独立子任务，比如归并排序和快排。
递推：递推是把相同的操作放在不同的数据上做，是天然的数据并行的数据域分解的思想，是GPU并行的核心思想。

在实际的工程中，

递归：递归应用在程序实际执行路径类似有限树或者有限图的情况中，完美契合自顶向下的设计思想。
递推：当处理大型数据或者执行大型程序时，存在关键路径需要按照步骤来，就需要递推。

在编译器中，通常递归和递推是重点优化的对象，所以我们要尽量写成递归跟递推的函数，使其转译执行的时候能正确识别和优化。

递归在C++，Java，Python的编译器可以实现 TCO的优化，TCO指的就是当一个函数调用是该函数的最后一步 (Tail Position) 时，编译器识别到函数的范围值是一个尾调用时，它知道当前函数的栈帧不再需要了。因此，它不会创建新的栈帧，而是重用前一个栈帧，把返回值重写进去，省略了重新开一个栈帧的开销。

int factorial(int n) {
  if (n == 0) {
    return 1;
  }
  // 不是尾调用：
  // 在 factorial(n-1) 返回后，
  // 必须执行 "n * [返回结果]" 的乘法操作。
  return n * factorial(n - 1); 
}

// ================================================================================================================

// 辅助函数
int factorial_helper(int n, int acc) {
  if (n == 0) {
    return acc;
  }
  // 这是尾调用：
  // 函数的返回值 *就是* 递归调用的返回值，
  // 没有任何后续操作。
  return factorial_helper(n - 1, n * acc);
}

// 供用户调用的主函数
int factorial(int n) {
  return factorial_helper(n, 1);
}

递推的优化非常多，最常见的就是循环不变量往外提：

// x 和 y 的值在循环内不变
int x = 10;
int y = 5;
for (int i = 0; i < n; i++) {
    // (x * y) 是循环不变量，但在这里被计算了 n 次
    array[i] = data[i] + (x * y); 
}

// =========================================================================================================

int x = 10;
int y = 5;

// 1. 将不变量计算“外提”
int invariant_result = x * y; // 只计算 1 次

for (int i = 0; i < n; i++) {
    // 2. 在循环内重用结果
    array[i] = data[i] + invariant_result;
}

除此之外，还有展开循环的操作，主要是避免CPU分支预测失败导致的代价和给出并行执行的空间

// 循环执行 100 次
for (int i = 0; i < 100; i++) {
    a[i] = b[i] + c[i];
}

// ==============================================================================================

// 循环现在只执行 25 次
for (int i = 0; i < 100; i += 4) {
    // 循环体被复制了 4 次
    a[i]   = b[i]   + c[i];
    a[i+1] = b[i+1] + c[i+1];
    a[i+2] = b[i+2] + c[i+2];
    a[i+3] = b[i+3] + c[i+3];
}
// 编译器还会自动处理 "收尾" (tail)，
// 以防 n 不是 4 的倍数。

最后一个是编译器的自动想量化和SIMD。编译器会讲程序员的标量循环改成SIMD的向量循环，而SIMD是现代CPU支持的单指令多数据的指令集，能一次处理4、8或16个元素。
所有的优化都需要一条前提，那就是不能有循环依赖(Loop-Carried Dependencies, LCD)

// 这个循环无法被向量化
for (int i = 1; i < n; i++) {
  // 依赖于上一次迭代的结果 A[i-1]
  A[i] = A[i-1] + B[i]; 
}

树

以二叉树为例，常见的代码如下：

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

// 二叉树的遍历
void preOrder(TreeNode *root) {
    if (root == NULL) return;
    cout << root->val << " ";
    preOrder(root->left);
    preOrder(root->right);
}

福生无量摸鱼天尊

算法 —— 基础篇：树图、高精度、二分和dp

递归递推

树